Statistische Äquivalenztests und Tests auf Nichtunterlegenheit
Das Äquivalenzproblem
Der Nachweis der Gleichheit von Eigenschaften zweier Gruppen oder der Nachweis, dass eine Differenz = 0 ist, sind gar nicht so selten Gegenstand von klinischen Studien oder Experimenten: So soll z. B. gezeigt werden, dass eine kostengünstigere Therapie genauso wirksam ist wie eine kostenintensive, dass sich ein bestimmtes physiologisches Merkmal in zwei Gruppen nicht unterscheidet, oder dass sich in einer Robustheitsuntersuchung die Messwerte gegenüber der ungestörten Messung nicht wesentlich ändern.
Der klassische Untersuchungsgegenstand ist die Bioäquivalenzprüfung bei Arzneimitteln. Hier wird untersucht, ob sich die durch eine Fläche bzw. deren Peak (siehe Abb.) charakterisierten Zeitkurven des Blutgehaltes von zwei verschiedenen Verabreichungsformen eines Arzneimittels nicht unterscheiden.
Wie die Differenz kann man auch den Quotienten zweier Größen betrachten: dann ist ein Verhältnis = 1 Ausdruck der Äquivalenz. Bei dem Bioäquivalenznachweis ist das beispielsweise der Fall. Eine weitere Anwendung ist der Nachweis der Äquivalenz der diagnostischen Güte zweier diagnostischer Tests: Die Äquivalenz von Sensitivität und/oder Spezifität wird über die Ratios rTPF (Verhältnis der "true positive fractions" TPF, TPF=Sensitivität) und rFPF (Verhältnis der "false postive fractions" FPF, FPF=1-Spezifität) gefasst, die im Idealfall 1 ist.
Das Nichtunterlegenheitsproblem (non inferiority)
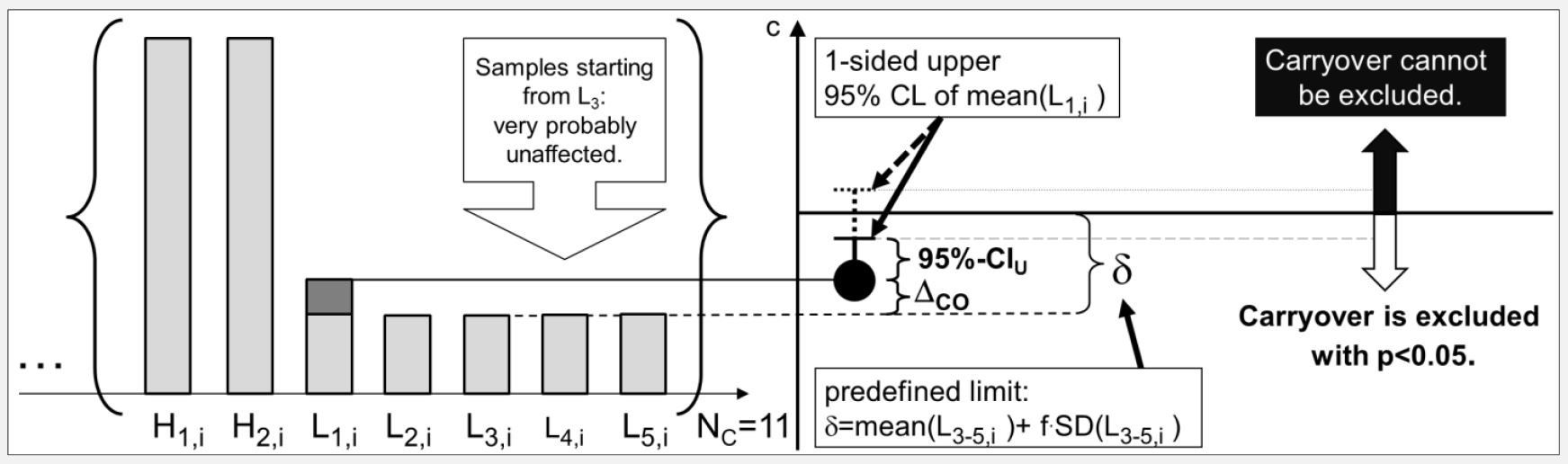
Es sei kurz auf ein verwandtes Problem hingewiesen, der Nachweis der Nichtunterlegenheit. Dies wird betrachtet, wenn Äquivalenz nur in eine Richtung von Interesse ist (keine Verschlechterung), aber eine Überlegenheit (und damit Abweichung von der Äquivalenz in eine Richtung) kein Problem oder sogar gewünscht ist. Ein Beispiel ist der Nachweis des fehlenden Carry-Overs bei Messgeräten in der Laboratoriumsmedizin: hier interessiert nur, dass Proben mit einer hoher Konzentration nicht zu fälschlich erhöhten Werten von später gemessenen Proben führen (z. B. in Folge von Verschleppung). Ein anderes Beispiel ist der Vergleich von Nebenwirkungen, diese sollten im Vergleich nicht häufiger anzutreffen sein, ein geringeres Auftreten ist dagegen kein Problem.
Vorgehen beim Äquivalenztest
Will man Äquivalenz zeigen, würde man zunächst von einer Differenz = 0 ausgehen. Das ist aber der Idealfall, real wird man einen gewissen Bereich zugelassen, innerhalb dessen eine Differenz als nicht relevant betrachtet wird. Es wird also ein um 0 liegender Äquivalenzbereich festgelegt, der durch Äquivalenzlimits begrenzt wird.
Ein statistischer Nachweis kann so geführt werden, dass der sogenannte Schätzer (z. B. ein Mittelwert) zusammen mit seinem Unsicherheitsbereich (beschrieben durch das Konfidenzintervall) betrachtet wird. Das Konfidenzintervall muss innerhalb der Äquivalenzlimits liegen, um Äquivalenz zu zeigen (obere Abb.).
Alternativ wendet man statistische Hypothesentests an. Hier werden 2 Nullhypothesen formuliert: Die Mittelwert liegt unterhalb oder oberhalb der Limits (Abb. Mitte). Die Alternativhypothese nimmt dagegen die Lage der Differenz innerhalb des Bereiches an. Werden beide Nullhypothesen abgelehnt, so ist der Nachweis erfolgt.
Werden Mittelwerte betrachtet, so kommen zwei einseitige t-Tests zur Anwendung (TOST: two one sided t-tests [Schuirmann DJ. A Comparison of the Two One-Sided Tests Procedure and the Power Approach for Assessing the Equivalence of Average Bioavailability. J of Pharmacokinetics and Biopharmaceutics 1987; 15(6): 657-680]). Mittlerweile wird der Begriff TOST häufig als Synonym für Äquivalenztests generell verwendet, obwohl er sich streng genommen auf t-Tests und Mittelwertvergleiche bezieht. In vielen Softwareprogrammen ist nun der TOST zu finden. Unter dem Begriff TOST wird der Äquivalenz-Test-Ansatz mitverstanden.
Hinweis: Auf unserer Website können Sie zwei Excel-Tools
für die Anwendung des TOST-Äquivalenztests laden, inkl. Tabellierung von nötigen Stichprobenumfängen (Abb. unten).
Festlegung der Äquivalenzlimits
Das Hauptproblem bei der Durchführung der Äquivalenztests ist die prospektive(!) Festlegung der Äquivalenzlimits. Zunächst: dies ist eine inhaltliche und keine statistische
Fragestellung. Trotzdem nimmt die Festlegung der Äquivalenzlimits breiten Raum in der statistischen Beratung
ein. Weite Bereiche haben einen geringeren Stichprobenumfang zu Folge, und der Nachweis gelingt leichter. Andererseits kann die Validität des Nachweises eingeschränkt sein, und er wird z. B. von den Behörden nicht akzeptiert.
Man kann sich dieser Frage durch folgende Betrachtungen nähern:
- Welcher Unterschied ist nicht relevant?
- "A difference that makes no difference."
- Was ist die minimal interessierende Differenz (MID) - der Äquivalenzbereich sollte etwas kleiner sein, z. B. das 0,7 fache.
- Wie groß ist die Messunsicherheit oder die biologische Variabilität - auch hier gilt: der Äquivalenzbereich sollte kleiner sein.
Im Bereich von Bioäquivalenzstudien sind die Grenzen durch die Behörden festgelegt: "Decision in favour of bioequivalence will be accepted when the parametric confidence intervals do not exceed the limits of 80 and 125% for the ratio of AUC-values and for the ratio of Cmax-values. The decision procedure based on 90% confidence intervals."
Statistische Äquivalenztests als wichtiges Auswertetool bei der Methodenvalidierung
Bei Methodenvalidierungsexperimenten geht es häufig darum, nachzuweisen, dass eine Zielgröße =0 ist. Z. B. kann es bei einem Methodenvergleich das Ziel sein, zu zeigen, dass der Bias (=systematische Fehler) der Test-Methode gegenüber einer Vergleichsmethode vernachlässigbar (=0) ist. Oder bei einer Robustheits- bzw. Stabilitätsuntersuchung ist zu zeigen, dass keine relevanten Änderungen auftreten.
Das häufig anzutreffende Vorgehen: "Der Test auf Unterschied liefert keinen signifikanten Unterschied, also sind die Gruppen bzgl. des untersuchten Merkmals gleich" ist aus statistischer Sicht falsch. Ein solches Ergebnis ist zwar ein Anhaltspunkt, aber kein Nachweis. Denn es handelt sich um Signifikanztests, mit denen die Ablehnung der - die Gleichheit besagende - Nullhypothese nachgewiesen werden kann, nicht jedoch deren Annahme.
Wenn also das Ziel eines Projektes im Nachweis einer Äquivalenz besteht, sind die entsprechenden Tests angebracht: die Äquivalenztests.
Während in der Pharmaindustrie Studien mit dem Ziel des Nachweises einer Äquivalenz bzw. der Nichtunterlegenheit weit verbreitet sind, und seit jeher adäquat ausgewertet werden (seit den 90er Jahren werden die zugehörigen Tests dann als Äquivalenztests bezeichnet), tut sich die Community der Laboratoriumsdiagnostik ausgesprochen schwer, die Methodik einzuführen. Die erste uns bekannte Publikation [Lung KR, Gorko MA, Llewelyn J, Wiggins N. Statistical method for the determination of equivalence of automated test procedures. J Autom Methods Manag Chem 2003;25:123-7] fand keinen Niederschlag.
Wir haben ein entsprechendes Vorgehen bei Untersuchungen zum Carry-Over, beim Nachweis der Kommutabilität sowie für den Methodenvergleich publiziert [Keller T, Brinkmann T (2014). Proposed Guidance for Carryover Studies, Based on Elementary Equivalence Testing. Clin. Lab 7,1153-61; Keller T, Weber S
(2009): Statistical Test for Equivalence in Analysis of Commutability Experiments. CCLM 47, 376-377 (Download Poster); Keller T, Faye S, Katzorke T (2011): Statistical Test for Equivalence in Analysis of Method Comparison Experiments. Application in comparison of AMH assays. CCLM 49: 806 (Download Poster)].
Mittlerweile findet das Vorgehen langsam den Weg in die Community [Holland MD, Budd JR, et. al. (2017): Improved statistical methods for evaluation of stability
of in vitro diagnostic reagents, Stat Biopharm Res, 9:272-278], ), auch wenn der Test im Fall der Kommutabilität noch nicht als Äquivalenztest bezeichnet wird [Nilsson G, Budd JR, Greenberg N, Delatour V, Rej R, Panteghini M, Ceriotti F, Schimmel H, Weykamp C, Keller T, Camara JE, Burns C, Vesper HW, MacKenzie F, Miller WG (2018). IFCC Working Group Recommendations for Assessing Commutability
Part 2: Using the Difference in Bias Between a Reference Material and Clinical Samples. Clin Chem 64:455-464].
Abbildung: Carry-Over als Nichtunterlegenheitsproblem, Abb aus Keller T, Brinkmann T (2014). Proposed Guidance for Carryover Studies, Based on Elementary Equivalence Testing. Clin. Lab 7,1153-61